Cubical Type Theory: The Unit Interval and Paths

/ Uncategorized / By

In this blog post, we will be following the very excellent paper [1]. Anyone looking for a good introduction that focuses less on the formal proofs should definitely give it a read!

Let us consider the most important object in the study of homotopy theory, the unit interval, I. The way we analytically understand this object is as the set of real numbers between 0 and 1. But we wish to have a synthetic way of discussing it that does not require us to develop the real numbers, intervals and the topology on it. Is there a way to describe the features that this object has and to express those features via a type construction?

The answer is yes! Let’s see a chunk of Arend code first and then discuss.

\data I 
  | left
  | right
  \where {
    \func squeeze (i j : I) : I
      | left, j => left
      | right, j => j
      | i, left => left
      | i, right => i

    \func squeezeR (i j : I) : I
      | left, j => j
      | right, j => right
      | i, left => i
      | i, right => right
  }
Credit: Arend [2],  Prelude.ard

As we can see, the type (although usually people discuss I as a pre-type) has a left endpoint, and a right endpoint. Note though, that this is not the Booleans. To see why, let us consider the additional structure (that of a De Morgan algebra, see [3] for a more formal treatment) that has been provided to us.

    \func squeeze (i j : I) : I -- The function sqeeze takes two imputs from the interval and returns the "min{i j}."
      | left, j => left -- min{left, j} = left
      | right, j => j -- min{right, j} = j
      | i, left => left -- min{i, left} = left 
      | i, right => i -- min{i, right} = i

    \func squeezeR (i j : I) : I -- The function squeezeR takes two imputs from the unit interval and returns "max{i,k}."
      | left, j => j -- max{left, j} = j
      | right, j => right -- max{right, j} = right
      | i, left => i -- max{i, left} = i
      | i, right => right -- max{i, right} = right

It will turn our that we can show that left = right, that is we have not defined the booleans (with their respective boolean algebra). This is a new object!

But this is good news, at least we did not reinvent the Booleans and call then the interval. So let us move forwards with what seems to be an at least plausible construction of the unit interval.

Now let’s move on to the reason that we wanted the unit interval, namely paths. Traditionally a path is a function f : I \rightarrow X where X is some topological space and f is a continuous function. We say that f(0) = a is the left-endpoint of the path and that f(1) = b is the right-endpoint.
More abstractly then, we should say that given a type A and two points a \: b : A, that a path from a to b is a function f : I \rightarrow A such that f \: left \equiv a and f \: right \equiv b. In Arend that is 

\data Path (A : I -> \Type) (a : A left) (b : A right)
  | path (\Pi (i : I) -> A i)

That is, a term of Path A a b is a function (path) which takes arguments f : \Pi_{i : I} A_i. Which is exactly like our definition above! If you want to construct a path from point a to point b, then you must find a function (which is continuous in HoTT) which has those endpoints.

Now for our first theorem/definition. The constant path, which Arend calls idp, but which is often called refl_a.

Theorem: Let A be a type with term a : A. Then there is a path, which we call idp, from a to a.
Proof: Define the function \lambda (t : I), a. Which is clearly a path from a to a.
Before we go to Arend we will now switch to the typical convention of writing a=b in the case that there is a path from a to b. The reason for this choice is well-covered in the HoTT Book [4].

\func idp {A : \Type} {a : A} : a = a => \lam _ => a

One interesting thing to point out is that our proof that such a path exists also comes with a specific function. This is the nature of a proof-relevant theory, since there may actually be a lot of these functions, which type-check, and which may have different computational features. Thus, my choice of proof is actually relevant to the mathematics that I do with it in the future.

Now, let us confirm that our paths act as we would expect them to, by showing that they satisfy an equivalence relation. The astute reader will observe that we actually already showed that = is reflexive (see idp). But first we need some tools.

\func coe (A : I -> \Type) (a : A left) (i : I) : A i \elim i -- The function which takes a type family over I, a term of A left, and an arbitrary i and returns a term of A i.
  | left => a 
-- NOTE THAT THIS IS IN PRELUDE! That is, this definition could not be made by a user, since it is non-exhastive. This function is part of our foundations. 

\func transport {A : \Type} (C : A -> \Type) {a a' : A} (p : a = a') (b : C a) : C a' -- The transport takes a path in A and "lifts" it to a path between C a and C a'.
  => coe (\lam i => C (p i)) b right

Credit: Arend [2], Prelude.ard

This can be best visualized with the following box diagram (made with https://tikzcd.yichuanshen.de/).

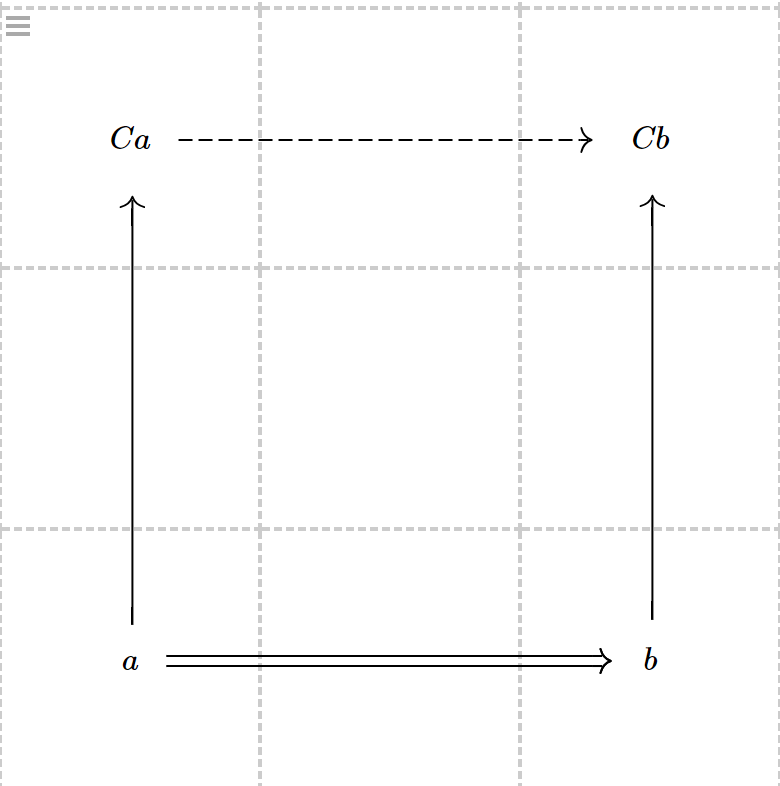
Where our double arrow indicates = and our single arrow indicate a function type.
Now let us show that paths induce functions.

\func induced {A : \Type} {C : A -> \Type} {a b : A} (p : a = b) : C a -> C b -- This is the principle that "puts the lid on every box."
  => \lam h => transport (C) (p) (h)

Now we are ready to show that it is an equivalence relation. 

\func path_refl {A : \Type} {a b : A} : a = a => idp -- Observe that we prooved relfexivity in secret! This is witnessed by the identity path!

\func path_symm {A :\Type} {a b : A} : a = b -> b = a =>
 \lam h => transport (\lam x => x = a) (h) (idp)  -- Let h be a path from a to b, then the transport on h is a path from b to a. 

\func trans {A : \Type} {a a' a'' : A} (p : a = a') (q : a' = a'') : a = a''
  => transport (\lam (x : A) => a = x) (q) (p) 
-- This last one is subtle, so lets break it down. We want a term of a = a'', so for our C : A -> \Type, we will choose 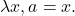\lambda x, a = x. Next we are required to give a proof that brings us to a point we know is equivalent to a'', so we use the path q. Lastly, given the first two pieces of data we need to give a proof of 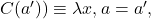C (a')) \equiv \lambda x, a = a', which we can do with p.

The last thing we will discuss before the next article is that paths (“or equality”) satisfy Leibniz’s Principle. This is brought up in the Arend Theorem Prover tutorial. Since there are many equivalence relations that do not act like equality, we must use this last principle to justify our choice of notation “=.” Note (for the unitiated that \Pi should be read as ‘forall’ and \Sigma should be read as ‘there exists a thing such that the next thing is true.’ 

\func Leibniz {A : \Type} {a a' : A}
              (f : (\Pi (P : A -> \Type) -> \Sigma (P a -> P a') (P a' -> P a))) : a = a' -- Given any predicate on A, if it is the case that there is a proof of P a -> P a' such that P a' -> P a, then a = a'. That is, loosely, if two terms satisfy the same propositions, then they are equal (indiscernible). 
  => (f (\lam x => a = x)).1 idp

Citations